1.通用的计算队列长度公式:(rear-front+QueueSize)%QueueSize
2.有序线性表顺序存储,删除一个元素平均需要移动(n-1)/2个元素
二、图
1.无向图的邻接矩阵是对应的,即图中的一条边对应邻接矩阵的2个非零元素
2.无向图:顶点i的度=邻接矩阵第i行元素的和
有向图:出度=邻接矩阵第i行元素的和 入度=邻接矩阵第j列元素的和
3.无向图:一个顶点的度是指关联于该顶点边的数目(该顶点相邻的顶点数)
4.连通无向图:任意两点是可达的
一个具有n个顶点的连通无向图至少有n-1条边
5.关键路径:源点到汇点权和最大的那条路径
最早开始时间:从源点到该活动对应点的最长路径的长度
6.具有n个顶点,e条边,用邻接表存储的图,其深度优先和广度优先时间复杂度均为O(n+e)
三、霍夫曼树
1.霍夫曼树(最优二叉树):带权路径长度最小的二叉树
2.构造算法关键步骤:在二叉树集合F中选取两颗根节点权值最小的树作为左右子树构造一颗新的二叉树(左右顺序没要求),置新的二叉树的根节点的权值为其左右子树上根节点的权值之和
3.性质:没有度为1的节点。因此n=n0+n2 n--总节点数 n0--度为0的节点个数(叶子节点) n2--度为2的节点个数 (度:节点拥有子树的个数)
4.树的带权路径长度:所有叶子节点的带权路径长度之和
节点的带权路径长度:该节点到树根之间的路径长度*节点的权值
路径长度:一个节点到另一个节点上有几根线
树的路径长度:根节点到每一个节点的路径长度的和
四、二叉树
1.二叉树性质:对任意一颗二叉树,有n0=n2+1
2.完全二叉树性质:具有n个节点的完全二叉树的深度为
构造堆时,将对应的一维数组转化成一颗完全二叉树
4.推导遍历结果:
前、中→后(唯一)
中、后→前(唯一)
前、后→不能确定一颗二叉树
5.二叉排序树(二叉查找树):左子树上所有节点的值小于根节点的值,右子树上所有节点的值大于根节点的值
对二叉排序树进行中序遍历可以得到一个有序序列
目的:并不是为了排序,而是为了提高查找、插入、删除关键字的速度
查找的比较次数=给定值的节点在二叉排序树中的层数
6.树的性质:对任意一颗树,它的总度数=节点数-1
6.树的性质:对任意一颗树,它的总度数=节点数-1
7.不同二叉树存储方式导致的空间浪费:
顺序存储:二叉树所占空间总数(数组)-节点数
链式存储:指针数目
8.平衡二叉树是一种特殊的二叉排序树,它的每一个节点的左右子树高度差最多等于1
9.二叉排序树的最小高度为完全二叉树的高度) 最大高度为每个节点占一层为n
最大高度为每个节点占一层为n
10.具有n个顶点的二叉树,如果用二叉链表存储,则空指针总数必定为n+1
11.树转化为二叉树时用孩子兄弟表示法
12.根节点高度算做1
五、分块索引
1.要求满足2个条件:1)块内无序 2)块间有序
2.索引项包含3个数据项:最大关键码(存储每一块中的最大关键字,好处:在它之后的下一块中得最小关键字也能比这一块中得最大的关键字大)、块长、块首指针
3.平均查找长度:
设n个记录的数据集被平均分成m块,每个块中有t条记录,显然n=m*t
设Lb为查找索引表的平均查找长度 = 
设Lw为块中查找记录的平均查找长度 =
则分块索引的平均查找长度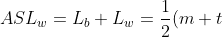+1=\frac{1}{2}(\frac{n}{t}+t)+1)
最佳的情况就是分的块数m=块中的记录数t
六、散列
1.线性再散列的公式为:Hi=(H(key)+di)%m 其中di=1,2,3,4,......
2.如果一个元素存入时,进行了N次散列,则相应的查找次数也为N
顺序存储:二叉树所占空间总数(数组)-节点数
链式存储:指针数目
8.平衡二叉树是一种特殊的二叉排序树,它的每一个节点的左右子树高度差最多等于1
9.二叉排序树的最小高度为完全二叉树的高度
10.具有n个顶点的二叉树,如果用二叉链表存储,则空指针总数必定为n+1
11.树转化为二叉树时用孩子兄弟表示法
12.根节点高度算做1
五、分块索引
1.要求满足2个条件:1)块内无序 2)块间有序
2.索引项包含3个数据项:最大关键码(存储每一块中的最大关键字,好处:在它之后的下一块中得最小关键字也能比这一块中得最大的关键字大)、块长、块首指针
3.平均查找长度:
设n个记录的数据集被平均分成m块,每个块中有t条记录,显然n=m*t
设Lw为块中查找记录的平均查找长度 =
则分块索引的平均查找长度
最佳的情况就是分的块数m=块中的记录数t
六、散列
1.线性再散列的公式为:Hi=(H(key)+di)%m 其中di=1,2,3,4,......
2.如果一个元素存入时,进行了N次散列,则相应的查找次数也为N
七、其他
1. 一维数组向二维数组转化
2. k分搜索
3. 在分支-界限算法中,通常采用广度优先搜索问题的解空间
4. 根据已知的表达式写对应的前(中、后)缀表达式
把表达式转化为一颗二叉树,对其进行前(中、后)序遍历
构造规则:
(1)操作数只在叶子节点上
(2)操作符是它们的根节点
(3)括号不构造到二叉树中
(4)构造树的顺序要遵循运算的顺序
5.逆波兰式就是后缀表达式
根据中缀构造二叉树比后缀容易
如果表达式第一位为符号,则可在前面加0 例如:-(a+b)*c-d → 0-(a+b)*c-d,且0-优先级高于*
1. 一维数组向二维数组转化
2. k分搜索
3. 在分支-界限算法中,通常采用广度优先搜索问题的解空间
4. 根据已知的表达式写对应的前(中、后)缀表达式
把表达式转化为一颗二叉树,对其进行前(中、后)序遍历
构造规则:
(1)操作数只在叶子节点上
(2)操作符是它们的根节点
(3)括号不构造到二叉树中
(4)构造树的顺序要遵循运算的顺序
5.逆波兰式就是后缀表达式
根据中缀构造二叉树比后缀容易
如果表达式第一位为符号,则可在前面加0 例如:-(a+b)*c-d → 0-(a+b)*c-d,且0-优先级高于*
八、堆、二叉排序树、霍夫曼树、中缀表达式小结
1.堆、二叉排序树都是从上往下构造
霍夫曼树和中缀表达式是从下往上构造
堆根据给出的序列按完全二叉树的形式构造,二叉排序树构造时需考虑左右节点间关系
2.霍夫曼树子节点小于父节点即可,不用考虑子节点之间关系
堆小于(大于)即可,不用考虑子节点之间关系
二叉排序树左<父<右

没有评论:
发表评论